前言
算子是深度学习计算图中的基本单元,负责执行各种数学和逻辑操作。在深度学习系统中,算子的实现对性能和效率有着至关重要的影响。为了解决多种硬件平台上的兼容性问题,Tenstorrent 算子的实现分为四个层次:用户层算子、基本算子、高层次算子(High-Level Kernel, HLK)和低层次算子(Low-Level Kernel, LLK)。本文旨在通过对这四个层次的详细解析,帮助读者理解 Tenstorrent 算子从设计到执行的全过程,以及各层次之间的关系和作用。在正式阅读本文之前,建议先阅读前文深入解析 TT-BUDA 架构及编译执行过程,了解 netlist 的格式以及 op type 字段是如何映射到 HLK 文件的。
用户层算子
当用户使用 PyTorch 等 AI 框架进行开发时,框架会提供一些算子(PyTorch 有2000多个算子),这些用户层算子往往较为复杂,而硬件厂商未必全部实现了,需要将用户层算子转换成硬件支持的算子。
基本算子(Netlist 支持的算子)
Netlist 支持的算子归纳如下:
| 基本算子类型(Netlist支持) | HLK 算子类型 |
|---|---|
| add | BinaryOp |
| subtract | BinaryOp |
| multiply | BinaryOp |
| quantization | BinaryOp |
| dequantization | BinaryOp |
| requantization | BinaryOp |
| maximum | BinaryOp |
| datacopy | UnaryOp |
| nop | UnaryOp |
| ethernet_datacopy | UnaryOp |
| splice | NaryOp |
| exp | SfpuOp |
| log | SfpuOp |
| sqrt | SfpuOp |
| gelu | SfpuOp |
| gelu_derivative | SfpuOp |
| reciprocal | SfpuOp |
| sigmoid | SfpuOp |
| dropout | SfpuOp |
| tanh | SfpuOp |
| square | SfpuOp |
| power | SfpuOp |
| sine | SfpuOp |
| cosine | SfpuOp |
| lrelu | SfpuOp |
| abs | SfpuOp |
| matmul | MatmulOp |
| reduce | ReduceOp |
| fused_op | FusedOp |
| embedding | EmbeddingOp |
| tilizer | TilizerOp |
| depthwise | DepthwiseOp |
| topk | TopkOp |
| drainer | DrainerOp |
| 查看 HLK 源码目录如下,和 HLK 算子的类型是一致的: |
tt-budabackend git:(4107668) $ ls hlks
binary depthwise drainer embedding inc matmul reduce sfpu splice
tilizer topk unary
由此可知,基本算子和 HLK 算子是多对一映射的。
观察 netlist 支持的算子列表,可以发现只实现少数的基本算子,而用户层算子需要分解为基本算子,才能出现在 netlist 中。
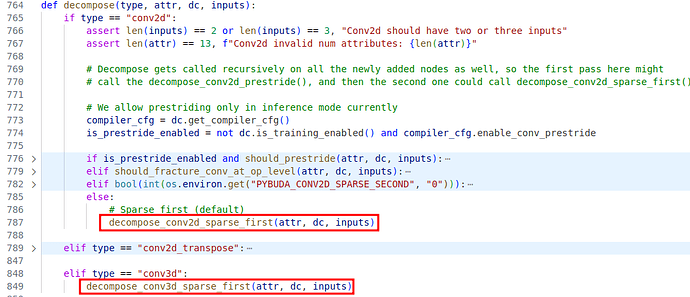
分解的过程在 pybuda 前端完成,每种用户层算子会有一个自己的 decompose 函数,用于将用户层算子分解成基本算子,卷积实现如下:
图1 卷积的 decompose 函数实现
二维卷积对应函数 decompose_conv2d_sparse_first,在此函数中,会将二维卷积分解成基本的算子如 matmul。
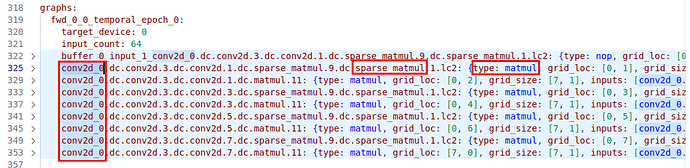
观察 resnet50 的网表文件 netlist_resnet50.yaml,如下所示:
图2 resnet50 netlist,conv2d 分解成 matmul
其中,conv2d 算子被分解成了多个 sparse_matmul 和 matmul 算子。
HLK(high level kernel)
HLK 作为高层次的算子库,是硬件无关的。即通过对硬件相关的 LLK 层算子进行封装或抽象,屏蔽硬件实现细节,便于支持多款 NPU。
以下是 HLK 中 add(批量加法)算子的实现示例,add 属于 BinaryOp,对应的 HLK 实现文件为 eltwise_binary_stream.cpp,代码如下:
// hlks/binary/eltwise_binary_stream.cpp
#include "hlks/inc/eltwise_binary.h"
TT_HLK_ALWAYS_INLINE void hlk_setup_kernel(tt_core* core_ptr, const hlk_args_t* args) {
hlk_binary_setup_kernel<BINARY_KERNEL_TYPE>(core_ptr, args);
}
TT_HLK_ALWAYS_INLINE void hlk_process_single_input(tt_core *core_ptr, const hlk_args_t *args) {
hlk_binary_main<BINARY_KERNEL_TYPE>(core_ptr, args);
}
不同的二元操作通过模板参数 BINARY_KERNEL_TYPE 来区分,BINARY_KERNEL_TYPE是通过头文件 hlk_compile_time_constants.h 传入,文件在编译时产生,譬如 add 算子,编译后会在头文件中对 BINARY_KERNEL_TYPE 赋值为 BinaryOp::Add。从上述实现可以看出,HLK 主要实现了 hlk_setup_kernel 和 hlk_process_single_input 这两个函数,这两个函数由入口函数调用,调用方式如下:
template<typename hlk_args>
void hlk_process_all_inputs(tt_core* core_ptr, const hlk_args *args, const int input_count) {
hlk_setup_kernel(core_ptr, args);
for (int i = 0; i < input_count; i++) {
hlk_pre_input_processing(core_ptr, i);
hlk_process_single_input(core_ptr, args);
hlk_post_input_processing(core_ptr);
}
}
uint run_kernel() {
regfile[p_gpr::DBG_CKID] = HLKC_MATH;
trisc_l1_mailbox_write((HLKC_MATH << 16) | KERNEL_IN_PROGRESS);
zeroacc();
setup_kernel();
hlk_process_all_inputs<hlk_args_t>(nullptr, &hlk_args, arg_loop_count);
}
其中run_kernel会被计算核的main函数调用,是入口函数。hlk_setup_kernel 做计算前的准备工作(如数据搬运),hlk_process_single_input 执行具体的计算。
展开二元操作的实现如下(简化版,仅处理一个 tile):
template<BinaryOp binary_op>
TT_HLK_ALWAYS_INLINE void hlk_binary_setup_kernel(tt_core *core_ptr, const hlk_args_t *args) {
hlk_hw_config_two_operands(core_ptr, HlkOperand::in0, HlkOperand::in1, args->transpose);
// No effect on mul
const int acc_to_dest = args->gradient_op;
hlk_binary_op_init<binary_op>(core_ptr, HlkOperand::in0, HlkOperand::in1, args->transpose, acc_to_dest);
}
template<BinaryOp binary_op>
TT_HLK_ALWAYS_INLINE void hlk_binary_main(tt_core *core_ptr, const hlk_args_t *args) {
hlk_acquire_dst(core_ptr);
// wait input streaming already
hlk_wait_tiles(core_ptr, HlkOperand::in0, args->block_tile_dim);
hlk_wait_tiles(core_ptr, HlkOperand::in1, args->block_tile_dim);
// Add
hlk_binary_op<BinaryOp::Add>(
core_ptr,
HlkOperand::in0,
HlkOperand::in1,
0,
0,
0,
args->transpose);
// pop input streaming
hlk_pop_tiles(core_ptr, HlkOperand::in0, args->block_tile_dim);
hlk_pop_tiles(core_ptr, HlkOperand::in1, args->block_tile_dim);
// wait output data ready and push to output streaming
hlk_wait_for_free_tiles(core_ptr, HlkOperand::out0, args->block_tile_dim);
hlk_pack_tile_to_stream(core_ptr, 0, HlkOperand::out0);
hlk_push_tiles(core_ptr, HlkOperand::out0, args->block_tile_dim);
hlk_release_dst(core_ptr);
}
分析上述代码,hlk_binary_op 函数会调用底层的 FPU 指令,FPU 计算指令(ELWADD 批量加)需要从 SrcA、SrcB 读取数据,计算完成后将结果输出到 DST 目的寄存器,整个计算过程如下:
- 将数据从 L1 SRAM 拷贝到 SrcA、SrcB 源寄存器,对应 hlk_binary_op_init 函数。
- 执行计算,将结果输出到 DST 目的寄存器,对应 hlk_binary_op 函数。
- 将数据从 DST 目的寄存器拷贝到 L1 SRAM,对应 hlk_pack_tile_to_stream 函数。
hlk_wait_tiles 函数用于同步,等待 L1 SRAM 中数据准备好。
其中 HlkOperand::in0、HlkOperand::in1、HlkOperand::out0 是全局变量 operands 的坐标,operands 的填充在 setup_kernel 函数中调用 llk_setup_operands 函数完成,展开如下:
inline void llk_setup_operands() {
while (EPOCH_INFO_PTR->all_streams_ready == 0)
;
for (std::uint32_t n = 0; n < EPOCH_INFO_PTR->num_inputs; n++) {
// iterates through all streams that have stream->unpacker functionality (inputs + intermediates)
std::uint32_t stream_id = EPOCH_INFO_PTR->inputs[n]->stream_id;
std::uint32_t fifo_addr = stream_get_data_buf_addr(stream_id);
std::uint32_t fifo_size = stream_get_data_buf_size(stream_id);
std::uint32_t input = operand_to_input_index(stream_id_to_operand(stream_id));
operands[input].f.fifo_rd_ptr = fifo_addr;
operands[input].f.fifo_rd_base_ptr = fifo_addr; // used for reads from interm buffers only
operands[input].f.fifo_size = fifo_size;
operands[input].f.fifo_limit = fifo_addr + fifo_size - 1; // Check if there is overflow
operands[input].f.tiles_acked = 0;
operands[input].f.words_acked = 0;
operands[input].f.blocks_per_iter = 0; // number of ublocks written per k into interm buffer
operands[input].f.curr_block = 0; // current number of ublocks written into interm buffer
operands[input].f.num_iter = 0; // number of passes through interm buffer (aka k-1)
operands[input].f.curr_iter = 0; // current number of passes through interm buffer
volatile std::uint32_t tt_reg_ptr * phase_changed_ptr = get_operand_phase_changed_ptr(stream_id_to_operand(stream_id));
*phase_changed_ptr = 0;
std::uint32_t operand = stream_id_to_operand(stream_id);
if (operand_is_intermediate(operand)) {
operands[input].f.blocks_per_iter = EPOCH_INFO_PTR->mblock_m * EPOCH_INFO_PTR->mblock_n;
operands[input].f.num_iter = EPOCH_INFO_PTR->mblock_k-1;
std::uint8_t packer_operand = EPOCH_INFO_PTR->inputs[n]->packer_operand;
bool shared_buffer = (packer_operand >= OPERAND_OUTPUT_START_INDEX);
operands[input].f.accumulation_buffer = shared_buffer || // buffer sharing is enabled only if there is interm buffer with mblock_k>1
(!shared_buffer && (EPOCH_INFO_PTR->num_outputs==1)); // gradient accumulation buffer
}
}
}
EPOCH_INFO_PTR 是一个全局固定地址,属于 overlay blob,由 NOC overlay 硬件负责填充数据。每个 epoch 对应多个输入,llk_setup_operands 函数会将输入数据存放到 operands 数组中。随后,可以通过 HlkOperand::in0 此类索引访问 operands 数组获取输入数据。
虽然代码只有一份,但是不同功能的 RISC-V 核的同一份代码会被编译成不同的可执行文件,这是由UNPACK、MATH、PACK这三个宏配合条件编译来完成的, 以hlk_hw_config_two_operands 函数为例,展开如下:
TT_HLK_ALWAYS_INLINE void hlk_hw_config_two_operands(tt_core* core_ptr, int stream_a, int stream_b, int transpose) {
UNPACK(
llk_unpack_AB_hw_configure_disaggregated<IS_FP32_DEST_ACC_EN, STOCH_RND_TYPE>(stream_a, stream_b, transpose));
MATH(llk_math_hw_configure_disaggregated<IS_UNTILIZE_OUTPUT_EN>());
PACK(
llk_pack_hw_configure_disaggregated<IS_UNTILIZE_OUTPUT_EN, IS_FP32_DEST_ACC_EN, RELU_TYPE, RELU_THRESHOLD, IS_TILIZE_INPUT_EN>(16));
}
可以看出,使用了三个宏(UNPACK、MATH、PACK)包装了 llk 函数。宏将代码分成了三个部分,被宏包装的函数由对应的 RISC-V 核负责执行,例如:使用 MATH 宏包装的函数由计算核负责执行,UNPACK 包装的由解包核负责执行。
数据传输和计算是在不同的核上执行的,因此可以隐藏数据传输的延时。数据传输核(UNPACK、PACK)和计算核(MATH)并行工作,传输和计算同步完成,计算和通信的流水线最大化利用资源。它们之间使用信号量进行同步,信号量在L1 SRAM 上分配,有固定内存地址。
LLK(low level kernel)
LLK 作为低层次的算子库,是硬件相关的,面对上层提供统一的接口,每个硬件有自己的一份实现。LLK 层处理封装了低层次的算子库以外,还提供了底层的打包、解包接口,用于数据传输。
仍然使用 add 作为示例来演示 LLK 的实现,add 对应的指令是 ELWADD(eltwise add 批量加),简化后的 MATH 核实现如下,对应于 HLK 的hlk_binary_op 函数:
template<...> inline void eltwise_binary_configure_mop(...) {
ckernel_template tmp(outerloop, innerloop, TT_OP_ELWADD(0, broadcast_type, addr_mod, 0));
tmp.set_end_op(TT_OP_SETRWC(p_setrwc::CLR_A, p_setrwc::CR_AB, 0, 0, 0, p_setrwc::SET_AB));
tmp.program(instrn_buffer);
}
template<...> inline void llk_math_eltwise_binary(...) {
ckernel_template::run(instrn_buffer);
}
在上述代码中,构造了一个 ckernel_template 实例,并调用了 program 和 run 成员函数,这是调用自定义指令的统一方法,如 MATH、PACK、UNPACK 指令都是如此。代码中还调用了 TT_OP_ELWADD 和 TT_OP_SETRWC 两个宏,其展开如下(以下宏实现和指令描述都是 Grayskull 的):
#define TT_OP_SETRWC(clear_ab_vld, rwc_cr, rwc_d, rwc_b, rwc_a, BitMask) \
TT_OP(0x37, (((clear_ab_vld) << 22) + ((rwc_cr) << 18) + ((rwc_d) << 14) + ((rwc_b) << 10) + ((rwc_a) << 6) + ((BitMask) << 0)))
#define TT_SETRWC_VALID(clear_ab_vld, rwc_cr, rwc_d, rwc_b, rwc_a, BitMask) \
(ckernel::is_valid(clear_ab_vld, 2) && ckernel::is_valid(rwc_cr, 4) && ckernel::is_valid(rwc_d, 4) && ckernel::is_valid(rwc_b, 4) && ckernel::is_valid(rwc_a, 4) && ckernel::is_valid(BitMask, 6))
#define TT_SETRWC(clear_ab_vld, rwc_cr, rwc_d, rwc_b, rwc_a, BitMask) \
ckernel::instrn_buffer[0] = TT_OP_SETRWC(clear_ab_vld, rwc_cr, rwc_d, rwc_b, rwc_a, BitMask)
#define TTI_SETRWC(clear_ab_vld, rwc_cr, rwc_d, rwc_b, rwc_a, BitMask) \
INSTRUCTION_WORD(TRISC_OP_SWIZZLE(TT_OP_SETRWC(clear_ab_vld, rwc_cr, rwc_d, rwc_b, rwc_a, BitMask) ))
#define TT_OP_ELWADD(clear_dvalid, instr_mod, addr_mode, dst) \
TT_OP(0x28, (((clear_dvalid) << 22) + ((instr_mod) << 19) + ((addr_mode) << 15) + ((dst) << 0)))
#define TT_ELWADD_VALID(clear_dvalid, instr_mod, addr_mode, dst) \
(ckernel::is_valid(clear_dvalid, 2) && ckernel::is_valid(instr_mod, 3) && ckernel::is_valid(addr_mode, 4) && ckernel::is_valid(dst, 15))
#define TT_ELWADD(clear_dvalid, instr_mod, addr_mode, dst) \
ckernel::instrn_buffer[0] = TT_OP_ELWADD(clear_dvalid, instr_mod, addr_mode, dst)
#define TTI_ELWADD(clear_dvalid, instr_mod, addr_mode, dst) \
INSTRUCTION_WORD(TRISC_OP_SWIZZLE(TT_OP_ELWADD(clear_dvalid, instr_mod, addr_mode, dst) ))
这些宏将自定义指令 0x28 和 0x37 组成的指令序列写入 instrn_buffer 中。查阅自定义指令表如下:
ELWADD:
op_binary: 0x28
ex_resource: MATH
instrn_type: COMPUTE
src_mask: 0x3
arguments: *ELW_ARGS
description: "Elementwise add operation"
SETRWC:
op_binary: 0x37
ex_resource: MATH
instrn_type: COMPUTE
src_mask: 0x0
arguments: &SETRWC_ARGS
- name: BitMask
field_type: BIN
start_bit: 0
description: "bit mask (fidelity_phase_clear,rwc_d,rwc_b,rwc_a)"
- name: rwc_a
field_type: DEC
start_bit: 6
description: rwc A value
- name: rwc_b
field_type: DEC
start_bit: 10
description: rwc B value
- name: rwc_d
field_type: DEC
start_bit: 14
description: rwc DST value
- name: rwc_cr
field_type: BIN
start_bit: 18
description: "bit mask (apply values specified to RWC CR counters (Dest CToCRMode,Dest,SrcB,srcA) (Dest CToCrMode: 1: CR <= Counter + inc, 0: CR <= CR + inc)"
- name: clear_ab_vld
field_type: BIN
start_bit: 22
description: clear srcA and srcB valids indicating to unpacker that new data can be written in
description: "Set register word counters or CR counters"
SETRWC 指令用于更改SrcA、SrcB 的标识位,等待数据输入。更多自定义指令见文件源代码仓库中的配置文件 assembly.yaml。
SFPU 算子
如果按照使用的硬件来区分,HLK 算子可以分为 FPU(矩阵运算)算子和 SFPU(向量运算)算子。上面描述的是 FPU 算子的实现,SFPU 算子在数据传输和 LLK 实现方式上有所不同。
数据传输差异
在数据传输方面,SFPU 算子需要比 FPU 算子多进行一步,FPU 算子将数据从 L1 SRAM 拷贝到 SrcA 和 SrcB 即可,SFPU 需要在此基础上,增加一步,将数据从 SrcA 和 SrcB 拷贝到 DST 目的寄存器。因为 SFPU 算子会默认从 DST 寄存器获取输入数据,计算结果也会保存在 DST 寄存器中。
实现方式差异
与 FPU 算子需要手动组装自定义指令序列不同,SFPU 算子的实现依赖于 Tenstorrent 提供的 sfpi 接口,自定义编译器会将 sfpi 接口实现的算子翻译成在 SFPU 上执行的指令。
以下是 abs 算子的 sfpi 实现示例。其中 dst_reg[0] 表示 DST 寄存器组中下标为 0 的寄存器(向量寄存器)。输入数据保存在 dst_reg[0] 中,计算完成后覆盖输入数据。使用 vFloat 声明了一个向量浮点作为中间变量。由于dst_reg使用下标进行访问,是 4x16 row based,而 SrcA、SrcB 以及 DST 寄存器是基于 32x32 tile 传输的,所以sfpi函数处理数据时需要循环处理。更详细的sfpi api 请见参考链接中的官方文档。
template <bool APPROXIMATION_MODE, int ITERATIONS>
inline void _calculate_abs_()
{
// SFPU microcode
for (int d = 0; d < ITERATIONS; d++)
{
vFloat v = dst_reg[0];
dst_reg[0] = sfpi::abs(v);
dst_reg++;
}
}
使用sfpi接口可以实现自定义算子。由于 tt-buda 是面向 AI 开发者的框架,自定义算子的使用较为复杂,因此将会在后续的 tt-metal 教程中详细介绍自定义算子的实现方法。
总结
通过对用户层算子、基本算子、HLK 和 LLK 四个层次的详细解析,我们可以更深入地理解 Tenstorrent 算子的实现原理和工作机制。用户层算子需要拆解成基本算子,基本算子会映射到高层次算子库(HLK),而 HLK 层通过调用低层次算子库(LLK)来实现具体的功能,LLK 层直接与硬件交互,执行具体的计算操作。这种分层结构不仅提高了算子的可移植性和可维护性,还能有效地优化性能,充分利用不同硬件平台的计算能力。