背景
在探索 Dataflow 架构:从理论到芯片实现中我们了解了冯诺伊曼架构和数据流架构的主要组成,同时在执行模型,并行处理能力和能效等方面对比了两种架构的优劣势。而在Tenstorrent 数据流芯片 Grayskull 和 Wormhole 解析中我们了解了 Tenstorrent 数据流芯片 Grayskull 和 Wormhole 的具体硬件实现,知道了为了满足人工智能日益增长的计算需求,解决 AI 大模型应用中的内存墙问题,他们在硬件设计上所做的决策。那么 Tenstorrent 数据流芯片设计可否应用到其它的场景呢?在本文,我们将从架构和编程模型的角度深入对比 Tenstorrent 数据流架构和冯诺伊曼架构。说明 Tenstorrent 数据流架构相对冯诺伊曼架构的主要优势,并且探索在其它的应用场景发挥这些优势的可能性;最后我们会展示在各种场景都会使用的经典的函数矩阵乘法如何利用 Tenstorrent 数据流架构进行加速,并且对比其在冯诺伊曼架构上的加速比。
冯诺伊曼架构
冯诺伊曼架构是目前最为广泛采用的计算机体系结构之一,1945 年由数学家冯诺伊曼提出。架构主体是 core (控制 + 计算单元) + 存储 + IO 设备。
- 在计算部分,冯诺伊曼架构关键特点是顺序执行,即指令按程序中规定的顺序逐条执行。为了提高并行能力,单个核心上,以 CPU 为代表的架构通常采用指令级的并行,如指令 Pipeline,乱序,多发射,SIMD 之类的方案提升每秒执行的指令数;以 GPU 为代表架构,会有张量等计算加速单元,以 SIMT 的方式加速程序的执行。在芯片层级,两者都是通过更多的 core 之间的并行,每个 core 可以启动一个或者多个线程,达到加速程序的目的。当线程数多于核心数时,线程间的并行需要通过调度程序来管理线程的执行。
- 在存储方面,冯诺伊曼架构通常是集中式共享式内存架构,多个核心共同访问同一片地址空间。为了解决内存墙问题,通常会采用层级式的内存架构,利用多级 cache 来缓解程序的访存压力;另一方面解决内存墙的问题则需要带宽更高的内存和网络通路。
Tenstorrent 数据流架构
架构简介
Tenstorrent 数据流芯片 Grayskull 和 Wormhole 解析中有详细的硬件设计。这里简单回顾一下 Tenstorrent 数据流架构,它的主体结构可以分为 Tensix Core 和 mesh 网络
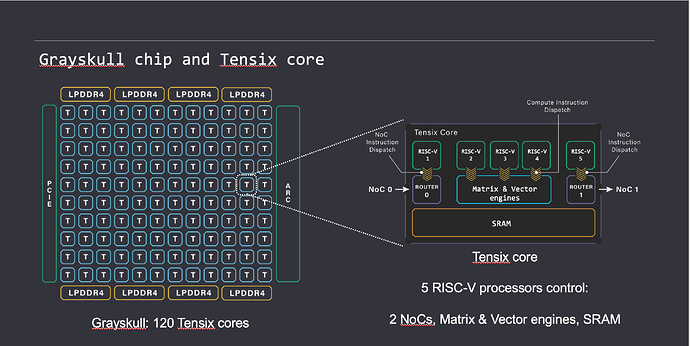
Tensix Core
- 5 个 Baby RISC-V Core (右侧绿色部分,RISCV-1…5),运行对应的 C/C++算子,发送指令给数据搬运引擎和计算引擎执行。其中 RISCV1 和 RISCV5 连通数据搬运引擎,负责数据在 Tensix Core 之间的流动;RISCV2-4 连通计算引擎,负责调用计算引擎对数据进行运算。
- 矩阵矢量引擎 (右侧蓝色部分),包含 FPU 和 SFPU 单元。其中 FPU 是张量计算单元,比如计算矩阵乘法;SFPU 是向量计算单元,用于各种杂项激活运算,如指数,平方根,softmax,topK 等。
- 数据移动引擎 (右侧紫色部分,NOC0,NOC1),负责控制 Tensix Core 之间或者 Tensix Core 和芯片的 LPDDR4 之间的数据传输。
- SRAM (右侧黄色部分),Baby RISC-V Core可以直接访问的地址范围,用于存放计算所需的数据和计算结束的结果。
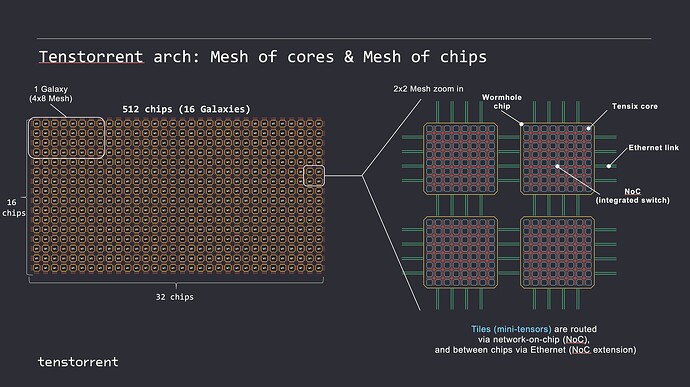
Mesh 结构
Tenstorrent 数据流芯片通过片上网络(NoC)和 Ethernet 可以透明地扩展到多个层次。即对于软件而言,看起来像是一个由 Tensix 核组成的 2D 同质网格,不需要关心芯片、服务器、机架这种层次结构。
编程模型
Core vs Thread
在 Tenstorrent 的数据流芯片中,编程单元是 Bare Metal Core,对应于 Tensix Core 里面的 Baby RISC-V Core。用户通过分配算子到这些 Bare Metal Core 来决定整个程序如何运行。每个 RISCV Core 是单线程运行的。在这种架构下,不存在上下文切换或复杂的线程调度。一旦算子被分配到一个 RISCV Core,它将一直运行直至整个程序完成,不会被其他线程中断或抢占。当算子规模远超单卡提供的规模上限,这时通过 flush Tensix Core,重新分配新的算子到 Tensix Core 达成算子切换。
Tensix Core 内部的 RISC-V Core 之间的同步通过 TT-Metalism API:"cb_reserve_back/cb_wait_front,cb_push_back/cb_pop_front"完成,Tensix Core 之间的数据同步可以通过信号量完成。
Tensix Core 内数据级并行
Tensix Core 的计算可以直接由 Baby RISC-V Core 执行,也可以通过 API 派遣到矢量引擎和矩阵引擎上计算。在 Baby RISC-V Core 上只能单条指令单条数据执行。相对的,Matrix Engine 和 Vector Engine (aka SFPU) 可以做 tile-base 的运算,即单条计算指令可以同时做 32x32 大小的标量运算。TT-Metalism 提供了大量的基础运算的 API,用户可以简单的使用这些 API 完成对于加速引擎指令的派遣。
Tensix Core 内核心级并行
Tensix Core 内部的 Baby RISC-V Core 是独立运行的,它们分别控制数据移动引擎和计算引擎的运行。负责数据移动 的 RISCV Core 可以异步的执行 tile 大小的数据移动指令,将数据读入 SRAM 和将 SRAM 的数据写到下一个 Tensix Core 或者内存。负责计算的 RISCV Core 可以异步的读取 SRAM 的数据到寄存器,计算后异步的将结果从目标寄存器打包到 SRAM。整个运算过程通过一些用于同步的 API 维持不同 RISC-V Core 之间数据的一致性。因此,在 Tensix Core 层级,DataMovement Engine 和 Matrix Engine 可以同时运行,数据和计算的延时可以重叠,实现 Tensix Core 内核心级并行。
芯片级 Tensix Core 并行
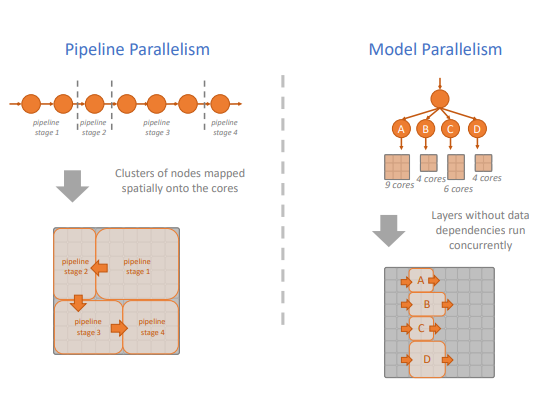
一个 Tenstorrent 的芯片上存在着大量的 Tensix Core。这些 Tensix Core 可以按照用户的意愿实现各种并行模式。如 Pipeline 模式:数据可以从一组 Tensix Core 进入,执行运算,然后将结果写入到下一组 Tensix Core。整个运算过程的中间结果不需要写回内存,这可以大大减少程序的内存墙问题;也可以采用多核的模式,将运算中的不同分支切分到不同组的 Tensix Core 同时运算,然后计算的结果或写回内存,或者继续采用 Pipeline 的方式传入到下一组 Tensix Core。整个划分的过程可以完全用户手动控制,也可以借助探索图编译器:实现高效的图计算中的图编译器自动完成任务的切分。
Mesh 结构 + 显式数据管理
-
显式数据管理:除了计算单元能力的差异,数据流动也是影响程序性能的主要因素。在 Tensix Core 中,数据移动是显式的,而且与计算引擎的操作是分离的。数据移动算子使用每个 Tensix Core 中的数据移动引擎将数据从相邻 Tensix Core 或 DRAM 搬运到 Tensix Core 的本地 SRAM,并触发计算引擎对数据进行操作。用户可以完全控制数据的来源,数据量的大小以及数据的目的地。比如用户可以将具有数据依赖的算子分配到邻近的 Tensix Core,减少数据在核间传递的延时。总之,用户可以完全自由的规划,优化和调试这些数据流图,相比于冯诺依曼架构,没有缓存,没有内存访问合并或传统架构中使用的其他复杂机制。
-
可扩展的网格架构。Tensix Core 通过 2 个数据移动引擎(NOC0 和 NOC1) 连接到网格中,每个 Tensix 核心都可以与网格中的任何其他 Tensix Core 以及 DRAM 甚至以太网连接的 Tensix Core 进行通信。这使得整个芯片可以支持多种数据布局和移动模式 (局域,行/列,最近邻居),应用到多种运算模式中,比如:
- 元素级操作在张量中的每个元素上完全是局域的,并且可以在没有任何数据移动的情况下实现。
- 矩阵乘法运算在矩阵的行和列数据存在明显的复用,因此可以通过在 Tensix Core 间进行广播达成复用的效果。
- 基于窗口的操作 (例如卷积),可以考虑与其邻居交换数据。
- 对于大型任务,如 HPC 中的算法,大规模神经网络,Tenstorrent 的多芯片模式与单芯片的架构在编程模型的角度上是完全一致的,因此可以很方便的 scale out。
近存运算,大容量 SRAM
- 无缓存机制:避免了传统架构中复杂的缓存一致性问题,通过直接在 SRAM 中操作数据来提高性能。Tenstorrent 芯片架构中,整个 SRAM 都处于一个单一级别,其巨大的容量可以用于存储输入,输出以及运算的中间结果。
- 每个 Tensix Core 中的高带宽和大容量 SRAM 是一种近内存计算形式。在其本地 SRAM 上运行的 Tensix 核心可以不必考虑 cache miss 的影响,充分发挥计算引擎的性能。
不同应用领域的潜力
根据前面对于 Tenstorrent 数据流架构和冯诺伊曼架构在编程模型的对比,我们可以看出 Tenstorrent 数据流架构在并行处理能力上的优势,同时因为灵活的网络结构和分布式的大容量 SRAM 带来的近存运算优势,其可以在很多领域发挥作用。下面我们将探讨一些算法及其在 Tenstorrent 数据流芯片上的加速潜力。
Monte Carlo 模拟
Monte Carlo 模拟算法是一种通过随机采样和统计分析来解决复杂问题的计算方法。在多个领域中有广泛的应用,如金融领域:用于期权定价,风险管理,投资组合优化等;物理学:用于加速器粒子碰撞实验的模拟;计算生物学:用于基因序列分析,药物研发等。
它的算法流程通常是
- 定义问题:确定要解决的问题,并将其转化为可处理的数学模型。
- 随机数生成:生成大量的随机数,这些随机数可以是均匀分布的或者根据问题的需求来自特定的分布。
- 模拟试验:使用随机数进行大量的模拟试验,记录每次试验的结果。
- 统计分析:对试验结果进行统计分析,计算出感兴趣的指标,如均值,方差,置信区间等。
- 结果近似:根据统计分析的结果来近似计算问题的答案。
在生成随机数,并进行统计分析流程中,算法本身通常会是循环操作,且大量的随机试验之间互相没有数据依赖。针对这种适合并行处理的算法,可以考虑将循环切块到不同的 Tensix Core,然后利用 Tensix 的矢量加速引擎,并行加速整个算法。
图算法
图算法是用于处理图这种数据结构的算法。图由节点和节点之间的连接边组成,可以用于表示各种关系和网络结构。邻接矩阵是一种常见的图表示方法,它使用一个二维数组来表示图,其中矩阵的元素表示节点之间是否有边以及边的权重。基于邻接矩阵的图算法,可以考虑利用 Tenstorrent 数据流架构在并行处理上的优势。比如多源最短路径算法 Floyd-Warshall 算法。其主要思想是通过逐步引入中间节点来更新最短路径。可以应用于路由优化,交通网络等。
const int INF = numeric_limits<int>::max();
void floydWarshall(vector<vector<int>>& dist) {
int n = dist。size();
for (int k = 0; k < n; ++k) {
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
if (dist[i][k] != INF && dist[k][j] != INF && dist[i][k] + dist[k][j] < dist[i][j]) {
dist[i][j] = dist[i][k] + dist[k][j];
}
}
}
}
}
针对 FloydWarshall 算法,我们可以按照矩阵乘法的 GPU 加速方式,将循环切块到不同的 Tensix Core,内层的条件判断操作,可以采用掩码操作,这样每个 Tensix Core 并行执行,加速引擎也可以并行加速。最后邻接矩阵的同一行和同一列的数据在计算中存在复用,可以考虑利用网络的广播操作,直接从对应的 Tensix Core 广播到同行和同列的 Tensix Core,减少数据的读写,进一步加速整个算法。
硬件仿真算法
硬件仿真算法是一种用于模拟计算机硬件行为的软件方法,不过在传统的冯诺依曼计算机上运行硬件仿真程序会遇到严重的内存墙问题。它通过在软件环境中模拟硬件电路的功能,性能和行为,来验证和测试硬件设计在实际物理实现之前的正确性和效率。这种仿真可以帮助设计者识别和修复潜在的错误,优化设计,并确保硬件在特定条件下的性能表现。
硬件仿真算法中各种软件实现的组件是相互独立,可以独自运行的,因此可以考虑使用并行加速;而指令需要在硬件中进行取指,译码,执行,访存,写回等操作,所以这些硬件组件又存在一定的数据依赖关系。组件需要从其余部分获取驱动组件运行的数据。因此可以考虑利用 Tenstorrent 芯片的网络的 pipeline 模式,整个硬件仿真算法完全映射到芯片,不同组件的数据依赖关系通过芯片上的网络进行连通。这种设计可以提高并行计算的能力,同时优化中间数据的读写过程,加速整个硬件仿真算法。
其它
数据科学和统计学主要关注数据的收集,处理,分析和解释。它们帮助解决各种实际问题,如预测趋势,发现模式,做出决策和优化资源等。在数据科学和统计学中,矩阵运算是核心工具之一,主要用于数据表示和数据运算。如矩阵乘法运算;矩阵分解:包括 LU 分解,QR 分解,SVD 分解等;统计量计算如协方差矩阵。这些矩阵运算都可以考虑使用并行处理的方式对算法进行加速。
图像处理和信号处理主要用于分析和操作图像及信号数据。这些领域的应用包括图像增强,特征提取,滤波和模式识别等。其中主要的卷积运算可以转化为矩阵的乘法进行并行加速。
高性能计算 (HPC) 领域专注于使用超级计算机和集群来解决计算密集型和数据密集型问题,如气象预测,分子模拟和大数据分析。除了基础的并行计算带来的优势,也可以考虑加速卡的可拓展性和交互方面的优势。
Tenstorrent 矩阵乘加速
前面分析了 Tenstorrent 数据流芯片对于不同算法的加速潜力,这里以一个具体的算法展示如何使用 Tenstorrent 数据芯片进行加速。
矩阵乘法在多个领域中有着广泛的应用,在 AI 应用领域,矩阵乘法是神经网络前向传播和反向传播中的基础操作,在图像处理领域,矩阵乘法用于图像变换和滤波等操作,在科学计算和工程实践中,复杂的数值计算和模拟中也会用到矩阵乘法等。因此,我们以矩阵乘法作为示例,展示 Tenstorrent 的数据流芯片如何对大型矩阵乘法进行加速。
测试平台
CPU:AMD Ryzen 9 3900X 12-Core Processor
- 12 核 24 线程
- 32KB L1,512K L2,16M L3
$: lscpu
Architecture: x86_64
CPU op-mode(s): 32-bit, 64-bit
Address sizes: 43 bits physical, 48 bits virtual
Byte Order: Little Endian
CPU(s): 24
On-line CPU(s) list: 0-23
Vendor ID: AuthenticAMD
Model name: AMD Ryzen 9 3900X 12-Core Processor
CPU family: 23
Model: 113
Thread(s) per core: 2
Core(s) per socket: 12
Socket(s): 1
Stepping: 0
Frequency boost: enabled
CPU max MHz: 4672。0698
CPU min MHz: 2200。0000
BogoMIPS: 7585。73
Flags: fpu vme de pse tsc msr pae mce cx8 apic sep mtrr pge mca cmov pat pse3
6 clflush mmx fxsr sse sse2 ht syscall nx mmxext fxsr_opt pdpe1gb rdts
cp lm constant_tsc rep_good nopl nonstop_tsc cpuid extd_apicid aperfmp
erf rapl pni pclmulqdq monitor ssse3 fma cx16 sse4_1 sse4_2 movbe popc
nt aes xsave avx f16c rdrand lahf_lm cmp_legacy svm extapic cr8_legacy
abm sse4a misalignsse 3dnowprefetch osvw ibs skinit wdt tce topoext p
erfctr_core perfctr_nb bpext perfctr_llc mwaitx cpb cat_l3 cdp_l3 hw_p
state ssbd mba ibpb stibp vmmcall fsgsbase bmi1 avx2 smep bmi2 cqm rdt
_a rdseed adx smap clflushopt clwb sha_ni xsaveopt xsavec xgetbv1 cqm_
llc cqm_occup_llc cqm_mbm_total cqm_mbm_local clzero irperf xsaveerptr
rdpru wbnoinvd arat npt lbrv svm_lock nrip_save tsc_scale vmcb_clean
flushbyasid decodeassists pausefilter pfthreshold avic v_vmsave_vmload
vgif v_spec_ctrl umip rdpid overflow_recov succor smca sev sev_es
Virtualization features:
Virtualization: AMD-V
Caches (sum of all):
L1d: 384 KiB (12 instances)
L1i: 384 KiB (12 instances)
L2: 6 MiB (12 instances)
L3: 64 MiB (4 instances)
NUMA:
NUMA node(s): 1
NUMA node0 CPU(s): 0-23
Tenstorrent:GraySkull 架构
- e150 系列
- 120 Tensix Core
- 1MB SRAM/(Tensix Core)
测试程序
我们选定编译器 O2 优化的单线程矩阵乘法程序作为基准。在 CPU 上考虑使用编译器自身 O3 优化,多线程,loop tiling,以及 AVX2 指令拓展进行加速。在 Tenstorrent 的芯片上,我们考虑多核,矩阵加速引擎,以及利用网络结构的广播操作进行加速。
原始矩阵乘法
矩阵乘法通常表示为三重循环的乘累加运算,这里为了利用 SIMD 指令加速,我们对乘数 B 的矩阵进行转置。整个矩阵的规模为 4096*4096。下面是使用 O2 编译运行的 Golden 矩阵乘法示例程序。
#define N 4096
// Transpose B matrix
for (int index = 0; index < N * N; index++) {
int i = index / N, j = index % N;
revB[i * N + j] = B[j * N + i];
}
// MatMul
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
for (int k = 0; k < N; k++) {
Result[i * N + j] += A[i * N + k] * revB[j * N + k];
}
}
}
多线程和 AVX2
在 x86 的多核的 CPU 上,我们可以考虑使用多线程切分整个计算任务到不同的线程并行运算;loop tiling 主要用来减少 cache miss;AMD 3900 支持 AVX2 拓展,可以使用单条指令完成 256 bit 数据的计算。优化后的代码如下:
void *ThreadProc(void *lpParam) {
MYDATA *pmd = (MYDATA *)lpParam;
int *A = pmd->A, *B = pmd->B, *C = pmd->C;
int block = pmd->block;
int begin = pmd->begin, end = pmd->end;
int i, j, k, i1, j1, k1;
for (i = begin; i < end; i++) {
for (j = 0; j < N; j += block) {
for (k = 0; k < N; k += block) {
for (j1 = j; j1 < j + block; j1++) {
__m256i res_vec = _mm256_setzero_si256();
for (k1 = k; k1 < k + block; k1 += 8) {
__m256i m1_vec = _mm256_loadu_si256((__m256i *)&A[i * N + k1]);
__m256i m2_vec = _mm256_loadu_si256((__m256i *)&B[j1 * N + k1]);
res_vec =
_mm256_add_epi32(res_vec, _mm256_mullo_epi32(m1_vec,
m2_vec));
}
int *p1 = (int *)&res_vec;
C[i * N + j1] +=
(p1[0] + p1[1] + p1[2] + p1[3] + p1[4] + p1[5] + p1[6] +
p1[7]);
}
}
}
}
return nullptr;
}
Grayskull
GraySkull 优化版本的完整代码请前往 Tenstorent TT-Metalium github 的矩阵乘示例 matmul_multicore_reuse_mcast 。TT-Metalium API 的使用会在 Dataflow 芯片和编译器从入门到进阶中的后续文章中介绍。下面我们将通过一些实验案例表明 Tenstorrent 数据流芯片的优势。
分组和广播
首先:考虑利用多核并行。将矩阵切块,每一个 Tensix Core 计算对应的块。
其次:在矩阵乘中,对应结果的 C 矩阵的每一行对应的 A 矩阵的行是相同的,因此我们可以复用 A 矩阵的行数据,同理每一列对应的 B 矩阵的列也是相同的。
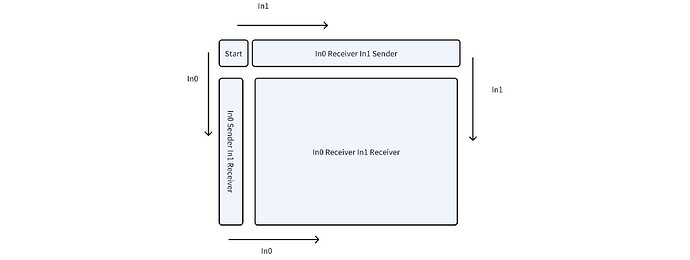
用 in0 和 in1 分别代表输入的 A 矩阵的行和 B 矩阵的列。芯片上的 Tensix core 可以分为四个部分。Start Core 会读入所需的 in0 行数据和 in1 列数据,同时作为 in0 行和 in1 列的发送者,通过 mcast 垂直向下将读入的 in1 列发送到 coregrid 的 left column,同样的将读入的 in0 行水平地 (从左到右) 发送到 coregrid 的 top row。Left column 核心所需的 in0 行数据会从 dram 读入,然后这些核心会作为 in0 行的发送者,将读入的 in0 行数据水平传播到其余的核心。同样的 top row 将负责将读入的 in1 列垂直的传播到每个核心。 整个过程只需要边缘的核心(Start Core,left column,top row)读入数据,可以有效的减少带宽以及读入数据所需的延时。
数据对比分析
| 优化选项 | int32 运行时间 | int32 加速比 | BF16 运行时间 | BF16 加速比 | |
|---|---|---|---|---|---|
| 单核 x86 (Golden) | O2 | 209.13s | 498.4s | ||
| 12 核 x86 (CPU 优化版) | O3 + 多线程 +Tiling + AVX2 | 1.86s | ~x112 (vs Golden) | 4.65s | ~x107 (vs Golden) |
| GraySkull | N/A* | 0.072 | ~x64.47 (vs 12 核 x86 CPU) |
数据说明:
- GraySkull 的数学计算引擎支持 BF16 的数据类型,但不支持 int32,所以 GraySkull 只展示了的 BF16 的数据。
- 多线程测试 16 线程结果最优,展示的为 16 线程的结果。
- GraySkull 的执行时间去掉了编译 kernel 的时间,仅考虑纯矩阵运算中数据搬运和计算时间。
分析:
在 CPU 上,编译器优化、多线程优化、loop tiling 与 AVX2 (SIMD) 相对原始的矩阵乘运算带来 107 倍的加速。在 GraySkull 上,通过并行处理以及广播操作带来的数据重用在 CPU 的优化版本基础上带来了 64 倍以上的加速。
总结
Tenstorrent 数据流芯片的多种数据并行方式,灵活的网络结构,以及大容量 SRAM 的近存计算模式,使得其在 AI 这种大规模数据处理的应用中展现出了强大的潜力。本文简单分析了这种架构相对于冯诺依曼架构的优势,探索了这种数据流芯片的架构在其它应用领域的潜力,抛砖引玉,希望读者能对数据流芯片的应用场景有更深入的理解,并能探索其在更多领域中的应用潜力。